I received my PhD in Preventive Medicine (Epidemiology) and Public Health, awarded Summa Cum Laude, from the University of Granada (UGR, Spain) and the ULB (Universite Libre de Bruxelles, Belgium). Also, I hold an MSc in Biostatistics from the University of Newcastle, Australia, an MSc in Epidemiology from the ULB and an MPH and health management from the UGR. After the completion of my Ph.D. in 2010, I moved to the Center for Infectious Disease Epidemiology and Research (University of Cape Town) as a postdoctoral fellow for two years. Afterwards, I moved to the Harvard School of Public Health (Department of Epidemiology), where I specialized in epidemiological methods from 2012 to 2015. I have also been trained as an Epidemic Intelligence Officer (EIS), and I worked as a field epidemiologist for several years in different African countries with Médecins Sans Frontières and GOARN-WHO during the Cholera epidemic in Haiti, 2010.
My research interests lie principally, but not exclusively in the field of epidemiological methods and comparative effectiveness research. At UCT, I used marginal structural models applied to large longitudinal data from Khayelitsha (HIV-Cohort) to assess the effectiveness of an observational, nonrandomized intervention Club of Patients. At Harvard, I used fixed effects methods in the context of the analysis of the components of the variance and within siblings design (observational cross-over) to evaluate the effect of a small fetoplacental ratio at birth on the risk of delivering a small for gestational age infant.
Currently, I am developing in collaboration with colleagues from the Cancer Survival Group (CSG) at the LSHTM data-adaptive methods for model selection and evaluation based on cross-validation techniques cvAUROC and applying advanced causal inference methods such as targeted maximum likelihood estimation TMLE to study social inequalities in cancer outcomes and survival.
Link to my list of publications (updated 2020): LIST
PhD in Epidemiology and Public Health, 2010
University of Granada, Spain
BSc in Mathematics and Statistics, 2023
Open University, UK
MSc in Data Science & Business Analytics, 2023
Nebrija University & INDRA, Spain
University Certificate in Biostatistics, 2019
Harvard University, Boston, USA
MSc in Biostatistics, 2015
University of Newcastle, Australia
Field Epidemiology Training Program (Epidemic Intelligence Officer Service), 2009
National Center of Epidemiology, ISCIII, Madrid, Spain
MSc in Epidemiology and Biostatistics, 2007
Universite Libre de Bruxelles, Belgium
Master in Public Health (MPH) and Health Management, 2005
University of Granada, Andalusian School of Public Health
MA in Social and Cultural Anthropology, 2004
University of Granada, Spain
University Diploma in Biostatistics, 2003
UNED University, Madrid, Spain
University Diploma in International Health, 2003
National Center of Epidemiology, ISCIII, Madrid, Spain
Obstetrics and Gynecology (Midwife), 1999
University of Granada
BSc in Health Sciences, 1993
University of Granada, Spain
Preprint The `projects` parameter in `content/publication/CCI.md` references a project file, `content/project/cci.md`, which cannot be found. Please either set `projects = []` or fix the reference.

Approximate statistical inference via determination of the asymptotic distribution of a statistic is routinely used for inference in applied medical statistics (e.g. to estimate the standard error of the marginal or conditional risk ratio). One method for variance estimation is the classical Delta-method but there is a knowledge gap as this method is not routinely included in training for applied medical statistics and its uses are not widely understood.
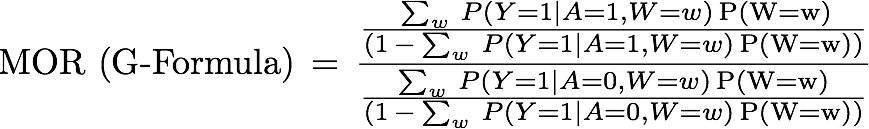
Effect modification and collapsibility when estimating the effect of public health interventions: A Monte-Carlo Simulation comparing classical multivariable regression adjustment versus the G-Formula based on a cancer epidemiology illustration: The American Journal of Public Health series Evaluating Public Health Interventions offers excellent practical guidance to researchers in public health. In the 8 part of the series, a valuable introduction to effect estimation of time-invariant public health interventions was given. The authors of this article suggested that in terms of bias and efficiency there is no advantage of using modern causal inference methods over classical multivariable regression modeling. However, this statement is not always true. Most importantly, both effect modification and collapsibility are important concepts when assessing the validity of using regression for causal effect estimation (https://github.com/migariane/hetmor/blob/master/README.md)

A collider for a certain pair of variables (outcome and exposure) is a third variable that is influenced by both of them. Controlling for, or conditioning the analysis on (i.e., stratification or regression) a collider, can introduce a spurious association between its causes (exposure and outcome) potentially explaining why the medical literature is full of paradoxical findings [6]. In DAG terminology, a collider is the variable in the middle of an inverted fork (i.e., variable W in A -> W <- Y). While this methodological note will not close the vexing gap between correlation and causation, but it will contribute to the increasing awareness and the general understanding of colliders among applied epidemiologists and medical researchers.
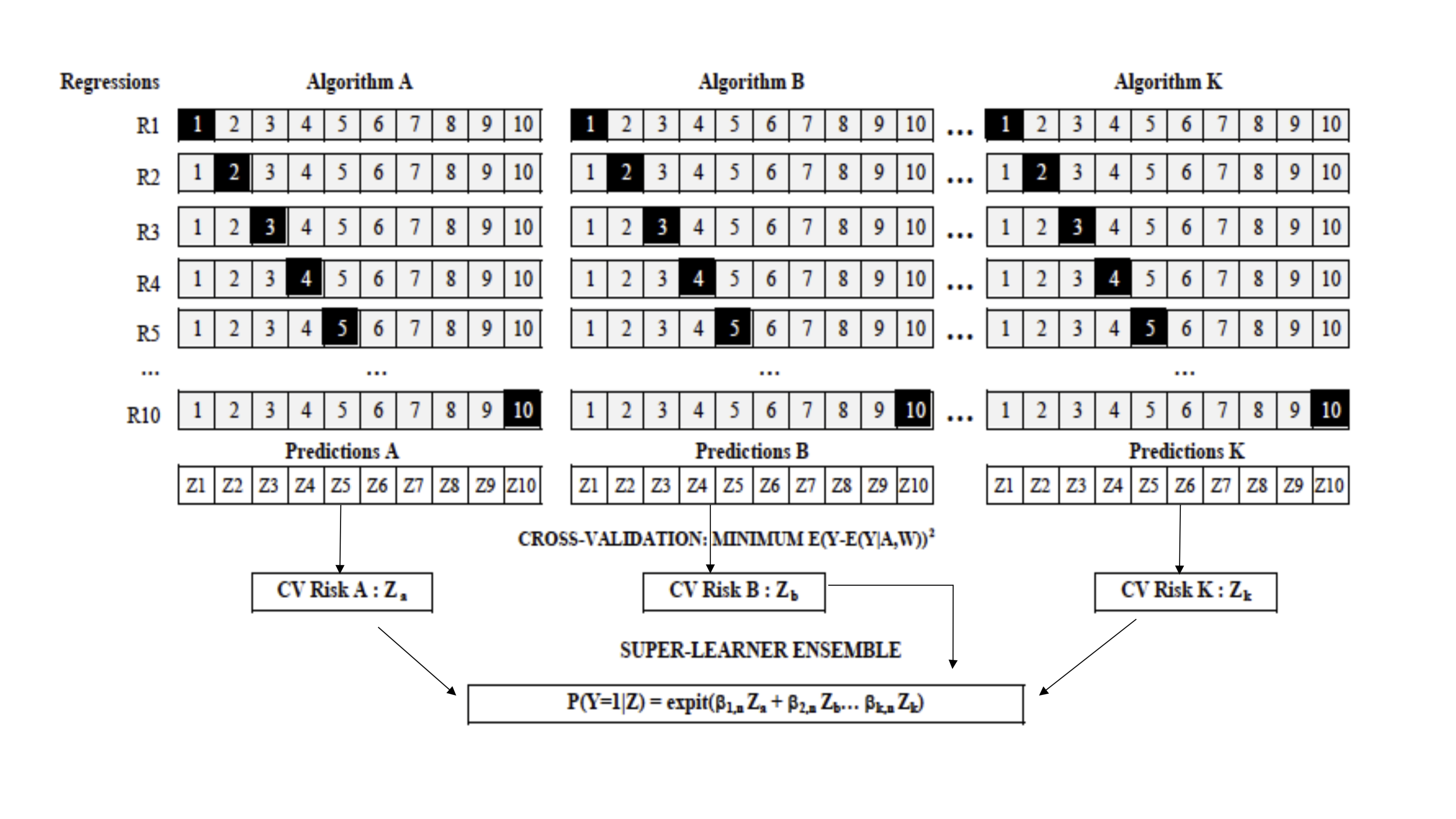
To improve model selection and prediction in cancer epidemiology data adaptive ensemble learning methods based on the Super Learner as a method for variable selection via cross-validation are suitable. To selection of the optimal regression algorithm among all weighted combinations of a set of candidate machine learning algorithms the ensemble learning method improves model accuracy and prediction.
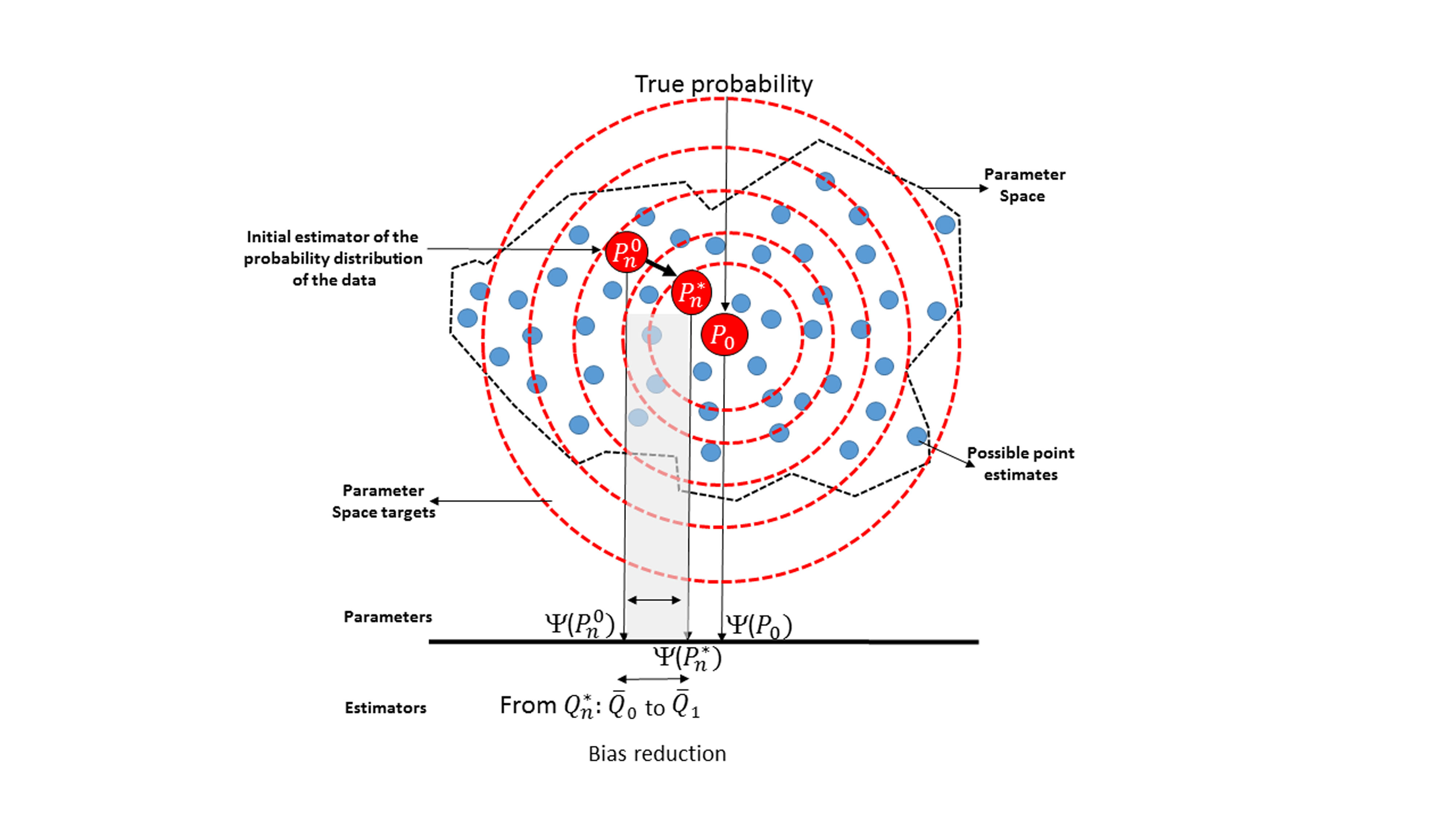
TMLE is a semiparametric doubly-robust method for Causal Infernece that enhances correct model specification by allowing flexible estimation using non-parametric machine-learning methods and requires weaker assumptions than its competitors.

In this tutorial the computational we show the implementation of different causal inference estimators from a historical perspective where different estimators were developed to overcome the limitations of the previous one. Furthermore, we also briefly introduce the potential outcomes framework, illustrate the use of different methods using an illustration from the health care setting, and most importantly, we provide reproducible and commented code in Stata, R and Python for researchers to apply in their own observational study. Available at https://arxiv.org/abs/2012.09920
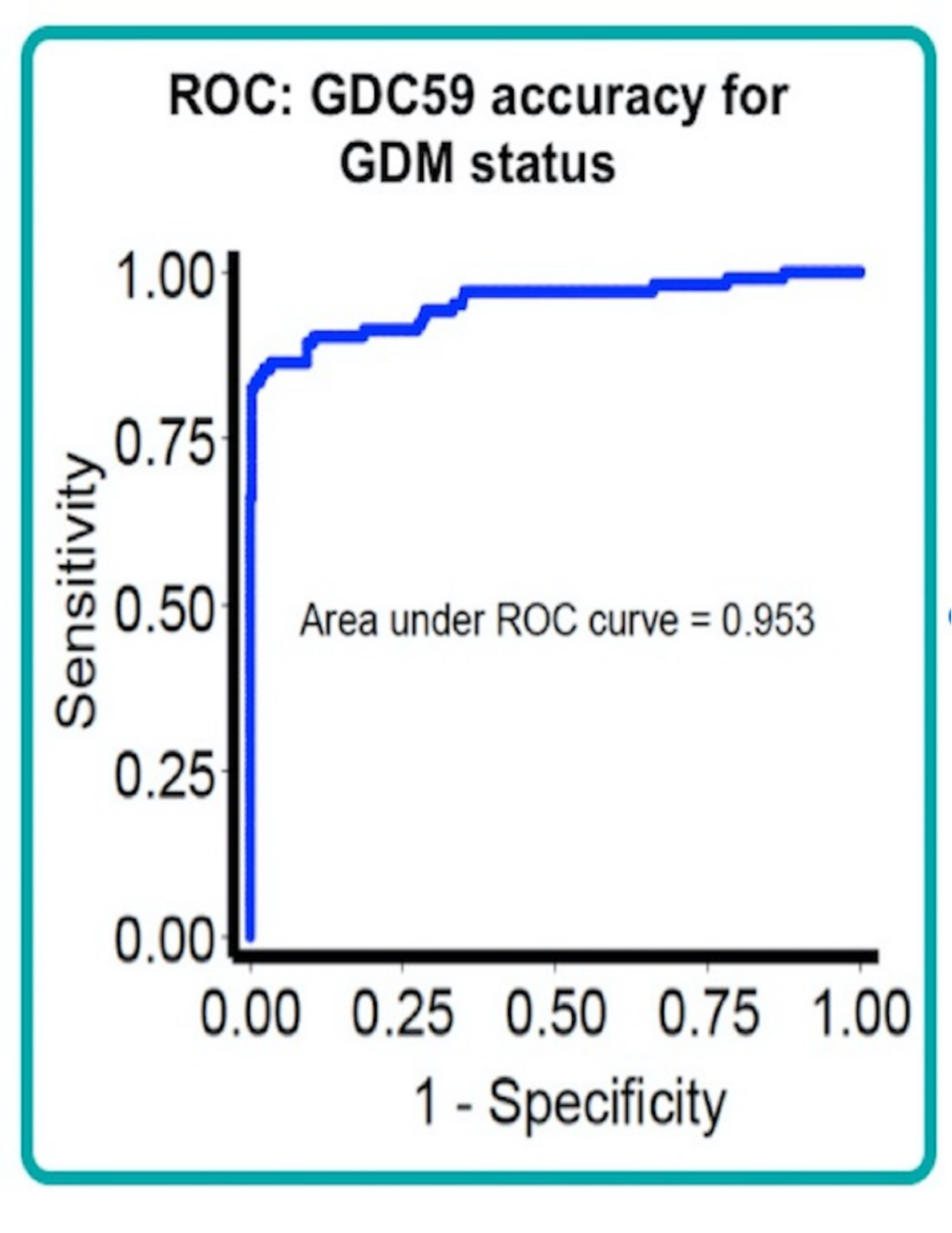
cvAUROC is a Stata program that implements k-fold cross-validation for the AUC for a binary outcome after fitting a logistic regression model. Evaluating the predictive performance (AUC) of a set of independent variables using all cases from the original analysis sample tends to result in an overly optimistic estimate of predictive performance. K-fold cross-validation can be used to generate a more realistic estimate of predictive performance.
I am a Distance Learning Module Organizer for the MSc in Epidemiology at the LSHTM and I teach in the following short courses:
EPM304 Advanced Statistical Methods in Epidemiology
Short Course: Introduction to Survival Analysis in Cancer Epidemiology: https://github.com/migariane/SVA-ULB
Introduction to Causal Inference and the Potential Outcomes Framework: https://ccci.netlify.com/
Computational Casusal Inference and Estimation using STATA (LSHTM): https://migariane.github.io/CIM.html
Also, I am developing software for teaching and scientific interests: